弦の張力について 2016.10
-序章-
張りの強い楽器・弱い楽器というものがよく語られます。
演奏者によって好みがあるので、どちらが良いというものではないですが、
演奏者は弦の張りの強さに敏感でこだわりを持つ人が多いです。
「張りの強さ・弱さ」を論じるだけでも実際の張力とボディー・ネックの剛性、
弦の種類、ナット/サドルの形、弦高と音色の関係など要素が多いですし、
数値では測れない「弦の感触」まで含まれます。
今回はギターになるべく近づけた状態で、ヘッド角度とサドルの高さを変え張力を計測しました。
結果として期待するのは
・ヘッド角度をつけるほど張力が大きくなる?
・サドルを高くすれば張力が大きくなる?
・ナットから糸巻きの距離が大きいほど張力が大きくなる?
以下の計測で答えを得ようと思います・・・
-Ⅰ- 実測
2種類のヘッド角度の違う張力測定器を作りました。
写真上がヘッド角8°で、下が16°です。 その他の条件は同じにしています。(弦長650㎜)
サドルから測定器までの角度は、実際の結び方でも測定可能ですが30°になり弦の安定に時間がかかるのと、摩擦抵抗が大きいので、5°にしてあります。(サドルの高さ3㎜の場合)
横から見るとヘッド角度の違いがわかります。
調弦が安定した時の張力を測定しました。 (安定するのに時間がかかるので新品は避け、2週以上張ったものを使用した)
測定誤差は測定器自体の誤差や、弦の両端、ナット/サドルの摩擦による抵抗などもあるので正確に出すのは難しいですが20グラム以内と結論づけました。

使用弦 サバレス 1-3弦 ニュークリスタル 4-6弦 カンティガ ノーマル
測定環境 27℃ 湿度50%
 計測結果
計測結果
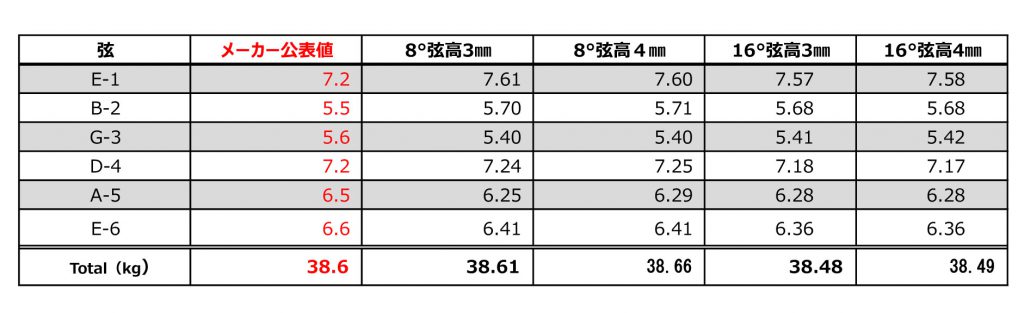
数回測り、平均を上記結果とした。 表の結果から、グラフを作り分析します。
※メーカー公表値はサバレス社が計算でなく実測したものです。
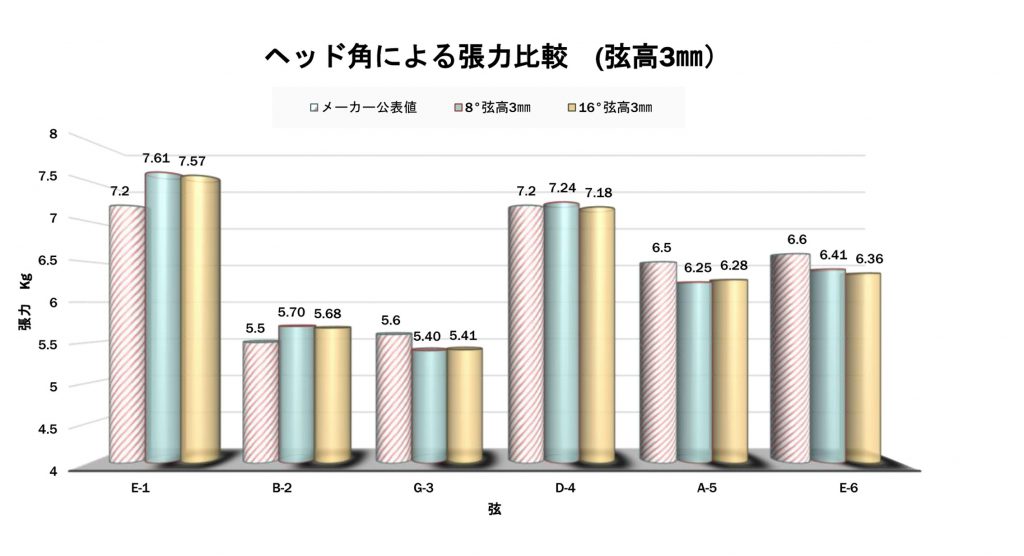
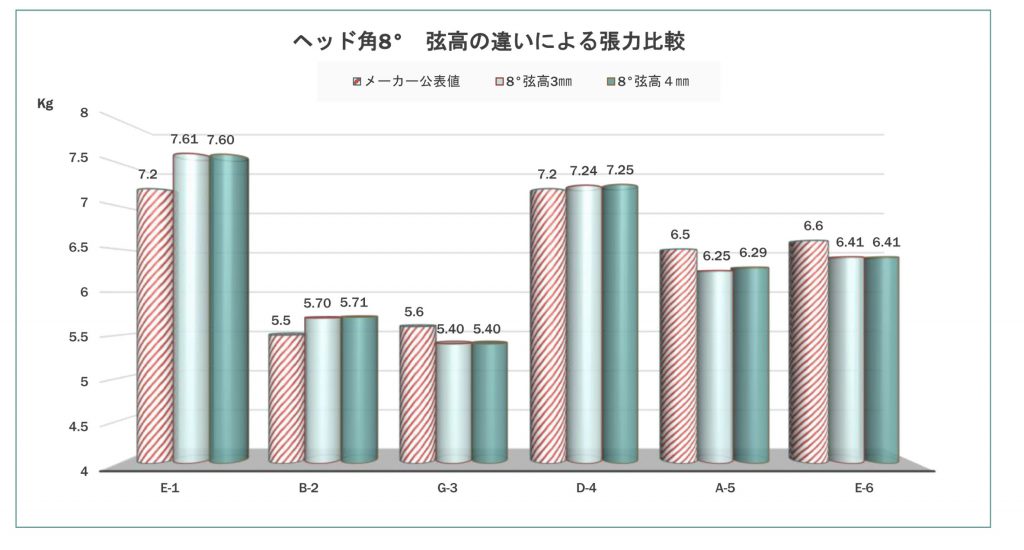
上のグラフは弦高3㎜でのヘッド角度による張力の変化を表します。 グラフから主に読み取れるのは
・角度による変化はほとんど無いと言って良いが(誤差の範囲)、わずかに8°のほうがトータルで張力が増える傾向がある
・とくに1弦はメーカー公表値よりかけ離れて大きい
・3弦、5,6弦など太めの弦は公表値より張力が低かった
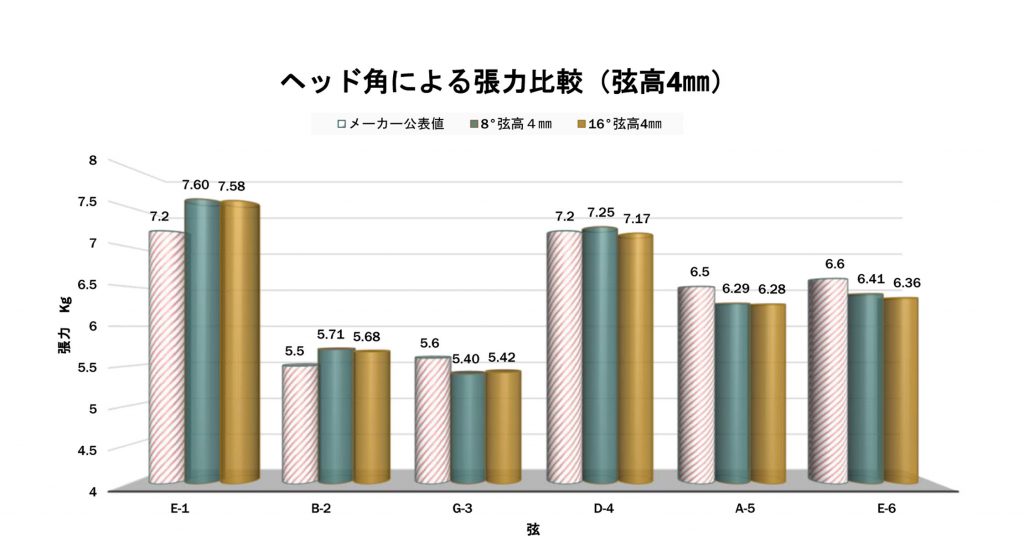
弦高4㎜でも同様の傾向があった。
・角度による変化はほとんど無いと言って良いが(誤差の範囲)、わずかに8°のほうがトータルで張力が増える傾向がある
・とくに1弦はメーカー公表値よりかけ離れて大きい
・3弦、5,6弦など太めの弦は公表値より張力が低かった
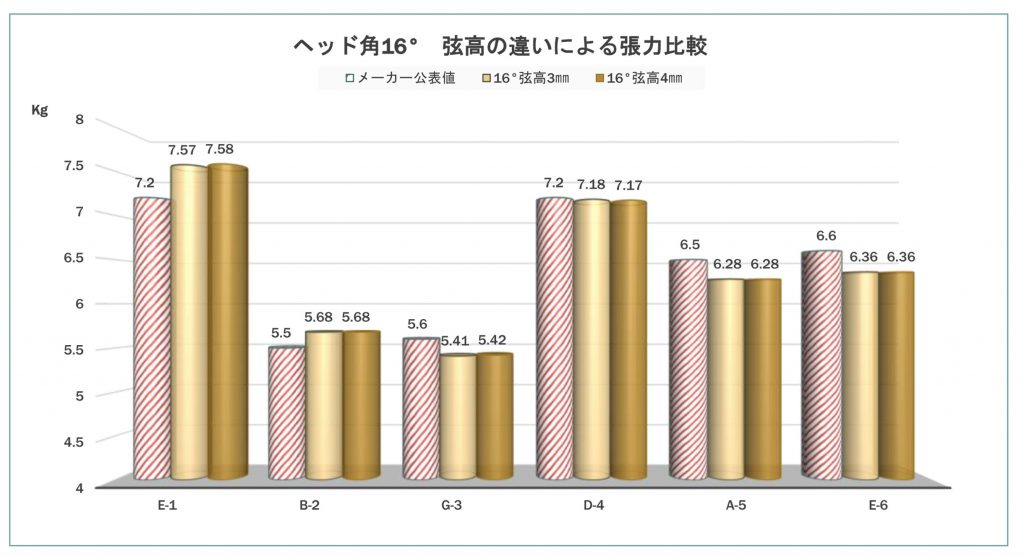
今度はヘッド角度を16°のままで弦高を変えた測定結果です。
弦高を高くすれば張力が高まるように期待しましたが、ほとんど変化はありませんでした。
同様にヘッド角度8°のときも、わずかに弦高4㎜のときに高くなる傾向があるが、ほぼ変化は無いと言って良いと思います。
次に、ナットから糸巻きの弦の長さが張力に影響するかを確かめます。
方法として、糸巻きの1弦に結んでいた弦を3弦で結び張力測定しました。
同様に糸巻きの3弦に結んでいた弦を1弦で結び測定しました。 4,6弦も同じです。
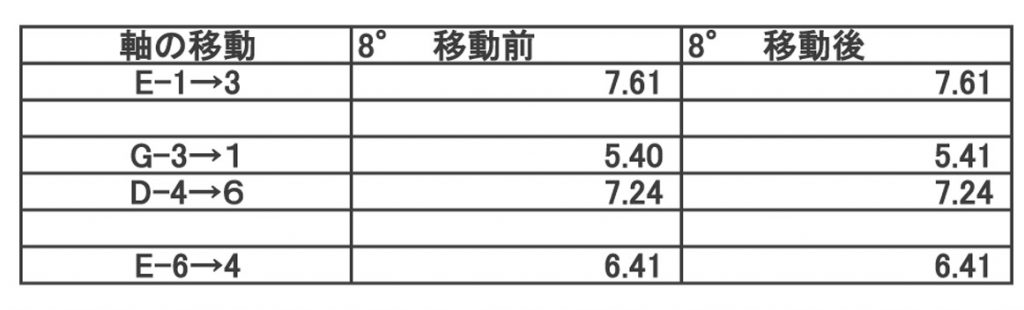
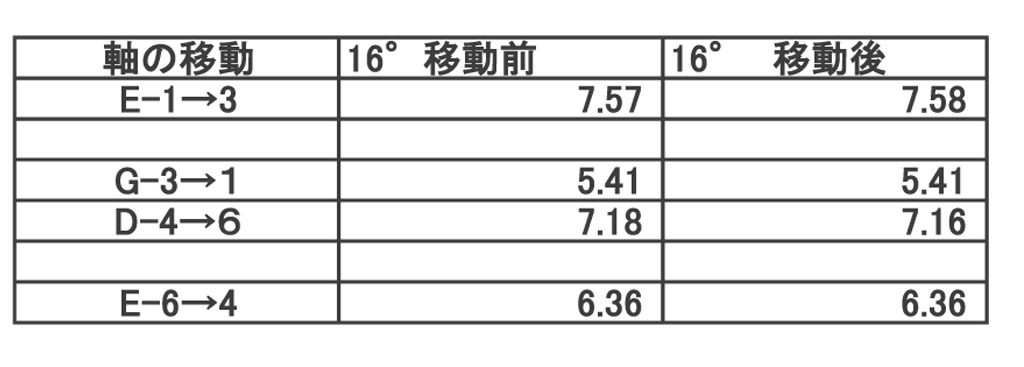
表の通り、ナットから糸巻きの長さは張力にほとんど影響がないことがわかった。
-ここまでの結論-
・ヘッド角度、サドル高を変えても思ったより張力の変化がなかった。
・ナットから糸巻きの弦長は張力に影響しなかった。
このことをふまえ、
「ヘッド角度や弦高、そしてナットから糸巻きへの弦長が張力に影響がない」ことを仮定する必要がでてきた。
この仮定を証明する必要がありますが、今宵は力尽きましたので近いうちに続きを書きます。
 -つづく-
-つづく-
-Ⅱ- 証明
復 活


2ヶ月のおまたせいたしました。 疲れ果てた その間に、ウェブサイト情報や専門家のご意見を聞くことができました。
上記の実測結果から定理を証明することにします。(色んな方のお力を借りて・・・)
実測結果から 「ヘッド角度や弦高、そしてナットから糸巻きへの弦長が張力に影響がない」
ということを証明するためには、物理の定理を理解する必要があります。
その定理とは
「ベクトルに、常にそのベクトルの方向に垂直な微小ベクトルを続けて積分すると、
ベクトルの方向が変わるがベクトルの大きさは変わらない」
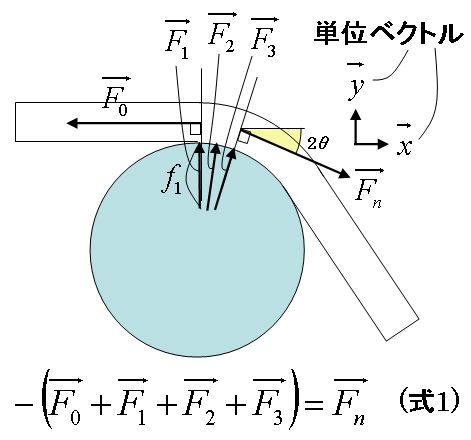
定理を数式で表すと、(式1)になります。 (張力Fnが、F0+F1+F2+F3 と釣り合う式)
(式1)を証明すれば、定理を証明したことになります。ただし弦の質や摩擦は考慮しません。
この定理は下記外部サイトに詳しく説明されています。


ここで、物理に苦手意識がある私は、物理の専門家 「柏木博士」の力を借りて式1を導いていただくことにした。
柏木博士はギターも弾かれ数々のコンクールに出場するほどの腕前です。
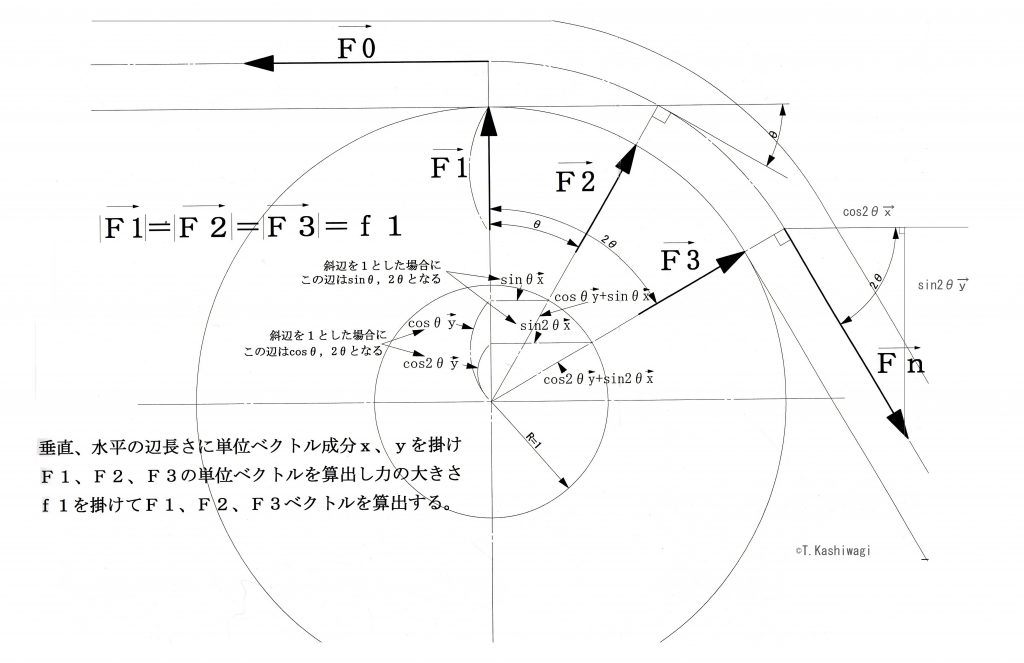

※数式の大文字Fの上にはベクトルの矢印(→)が本来あります。
式1を証明するためには、F0、F1、F2、F3、Fnを表示します。
注意が必要なのはFnで、nに数字を代入はできず、Fnという張力固有の値だと考える必要があります。
それをふまえ、yベクトルが逆方向なので、
Fn=fn(cos2θx-sin2θy) となる。

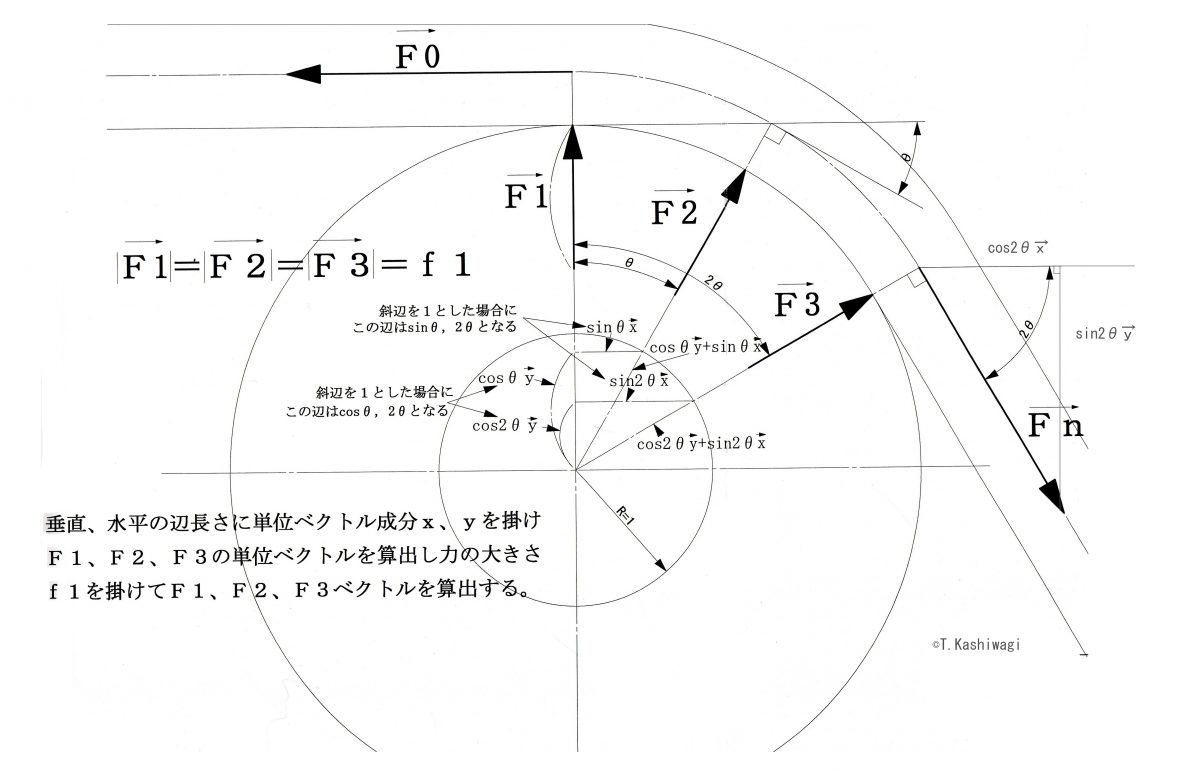
F0、F1、F2、F3、Fnの式を、式1に代入し計算します。



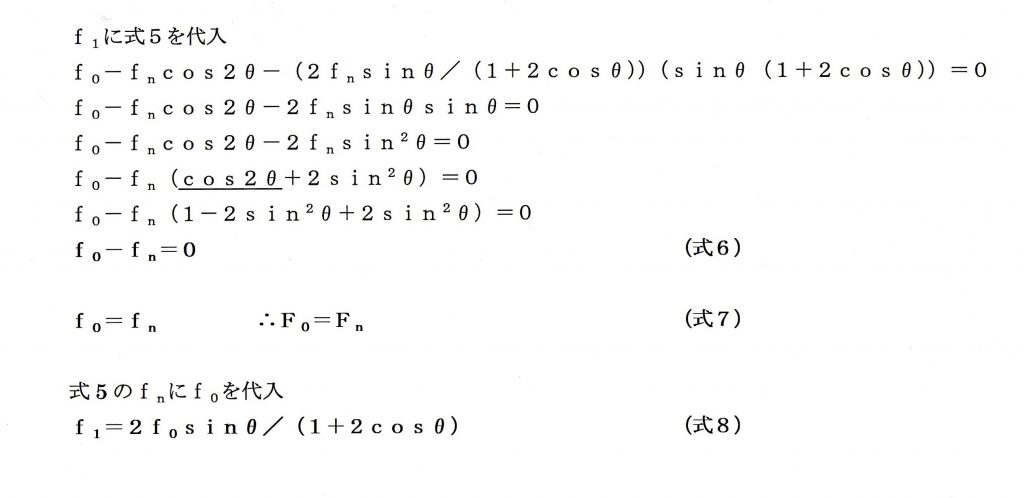

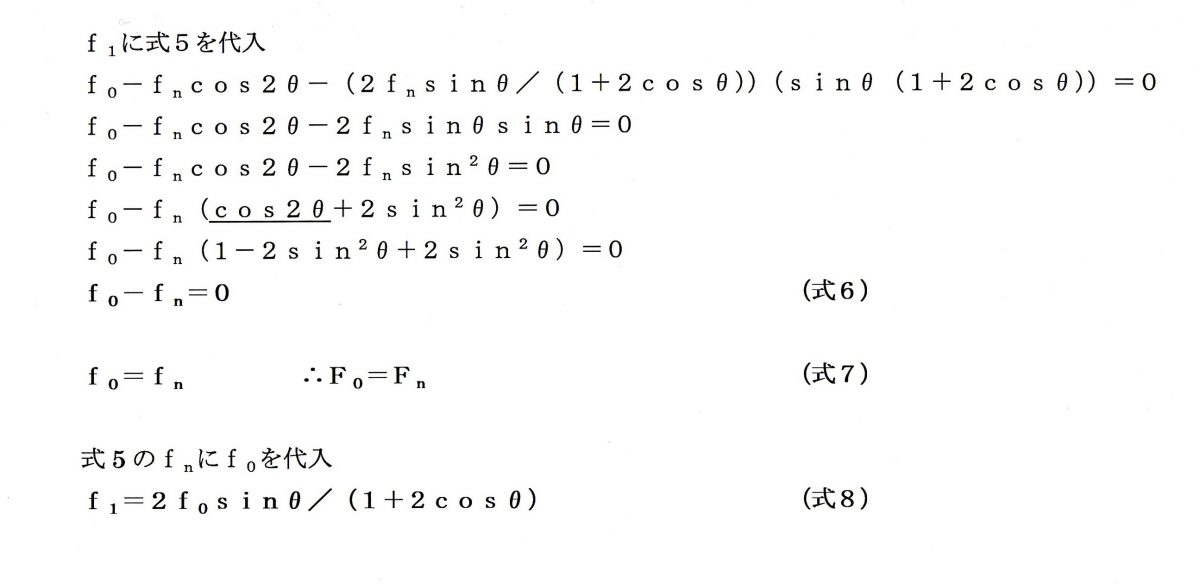
計算をしていくと、式7により定理は証明されました。
その過程で式5のFnにf0を代入することで、垂直抗力をあらわす式8が得られます。
この式8
f1=2f0sinθ/(1+2cosθ)
は、弦がナット・サドルを押し付ける力を表します。
かくして、弦の質や摩擦を考慮しない理論上では、『張力は弦長のみに支配され、ギターの構造による張力の変化はない』ことが証明された。
一方で、ギター構造の変化(弦の進入角)がナット・サドルに与える力を変化させることが理論上分かったのであった。そのご説明は次ページへ続きます。